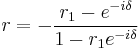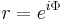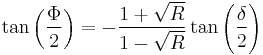Gires–Tournois etalon

In optics, a Gires–Tournois etalon is a transparent plate with two reflecting surfaces, one of which has very high reflectivity. Due to multiple-beam interference, light incident on the lower-reflectivity surface of a Gires–Tournois etalon is (almost) completely reflected, but has a phase shift that depends strongly on the wavelength of the light.

The complex amplitude reflectivity of a Gires–Tournois etalon is given by

r=-\frac{r_1-e^{-i\delta}}{1-r_1 e^{-i\delta}}

where r1 is the complex amplitude reflectivity of the first surface,

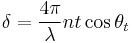
\delta=\frac{4 \pi}{\lambda} n t \cos \theta_t
n is the index of refraction of the plate
t is the thickness of the plate
θt is the angle of refraction the light makes within the plate, and
λ is the wavelength of the light in vacuum.

Nonlinear phase shift

Note that 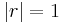|r| = 1, independent of 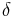\delta. This indicates that all the incident energy is reflected and intensity is uniform. However, the multiple reflection causes a nonlinear phase shift 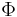\Phi. To show this effect, we assume 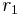r_1 is real and 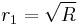r_1=\sqrt{R}, where R is the intensity reflectivity of the first surface.

Further, define the nonlinear phase shift 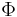\Phi through

r=e^{i\Phi}

and yield

\tan\left(\frac{\Phi}{2}\right)=-\frac{1%2B\sqrt{R}}{1-\sqrt{R}}\tan\left(\frac{\delta}{2}\right)

For R = 0, no reflection from the first surface and the resultant nonlinear phase shift is equal to the round-trip phase change (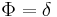\Phi = \delta) – linear response. However, as can be seen, when R is increased, the nonlinear phase shift 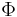\Phi gives the nonlinear response to 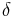\delta and shows step-like behavior. Gires–Tournois etalon has applications for laser pulse compression and nonlinear Michelson interferometer.

Gires–Tournois etalons are closely related to Fabry–Pérot etalons.

References